はじめに
「Power BI × Pythonで学ぶ重回帰回帰分析の実践」で作成した重回帰分析について解説します。重回帰分析を実施したものの、結果の読み解き方がわからない方に向けて、詳しく説明します。
方法(アプローチ・使用技術)
前回のおさらい
前回のおさらい
マーケティングデータから重回帰分析で学習モデルの生成を行い、ビジュアルを作成しました。本記事は重回帰分析の読み解き方から始めます。
重回帰分析とは
重回帰分析(Multiple Regression Analysis)は、複数の独立変数(説明変数)を用いて、1つの従属変数(目的変数)を予測する統計手法です。単回帰分析が1つの独立変数を用いるのに対し、重回帰分析では2つ以上の独立変数を用いる点が特徴的です。この手法は、売上の予測、医療データの分析、経済指標の予測など、幅広い分野で活用されています。
重回帰分析の精度を高めるためにすべきこと
今回は3点に焦点を当てて実施しています。
1.データの前処理(標準化)・・・変数のスケールを揃え、学習効率を向上
2.モデルの適合度評価(決定係数・RMSE)・・・モデルの適合度を評価
3.適切な特徴量の選択(回帰係数・p値)・・・重要な変数を選択し、多重共線性を回避
1.データの前処理(標準化)
標準化
重回帰分析では、異なる単位やスケールを持つ変数を適切に処理することで、モデルの精度を向上させることができます。標準化は、ロジスティック回帰分析と同様にデータの平均を0、標準偏差を1に変換する手法です。
X' = (X - μ) / σ
・X は元の特徴量の値
・μ は特徴量の平均
・σ は特徴量の標準偏差
・X' は標準化後の値
変数ごとにスケールが大きく異なる場合(例:売上額(万円)と従業員数(人))は標準化することが有効です。
2. モデルの適合度評価(決定係数・RMSE)
決定係数
重回帰分析の精度を測るために、モデルの適合度を評価する指標として決定係数とRMSE(Root Mean Squared Error)を活用します。
決定係数は、目的変数の変動をどれだけ説明できているかを示す指標です。
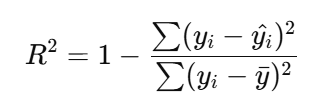
y(アイ[i]) :実際の値
y(ハット[^]) :予測値
y(バー[-]) :目的変数の平均値
R2 の範囲は0から1であり、1に近いほどモデルの説明力が高いことを表します。
RMSE(Root Mean Squared Error, 平均二乗誤差の平方根)
RMSEは、予測誤差の平均的な大きさを示す指標であり、モデルの精度を評価するのに役立ちます。
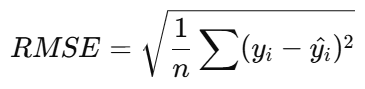
RMSEが小さいほど、モデルの予測精度が高いことを表します。
決定係数とRMSEの使い分け
・決定係数:モデルの説明力を見るのに適している。
・RMSE:誤差の大きさを評価するのに適している(低いほど良い)。
3.適切な特徴量の選択(回帰係数・p値)
回帰係数
回帰係数は、各説明変数が目的変数に与える影響の大きさを示します。
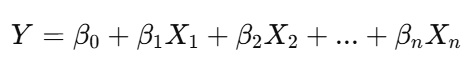
回帰係数の絶対値が大きい変数は影響力が大きいことを表します。
※回帰係数を評価するときは、スケールが異なる変数では比較が難しいため、標準化した回帰係数(標準化偏回帰係数)を使うと効果的です。
p値 ※"probability value" (確率値)
p値(p-value)は、説明変数が統計的に有意かどうかを判断するための指標です。
・p値が小さい(通常0.05未満)場合:その変数は統計的に有意であり、モデルに含めるべきです。
・p値が大きい場合:その変数は目的変数と関連が弱いため、除外を検討すべきです。
p値(P>|t|) を確認し、0.05以上の変数を除外することで、精度の高いモデルを構築できる。
グラフを読み解く
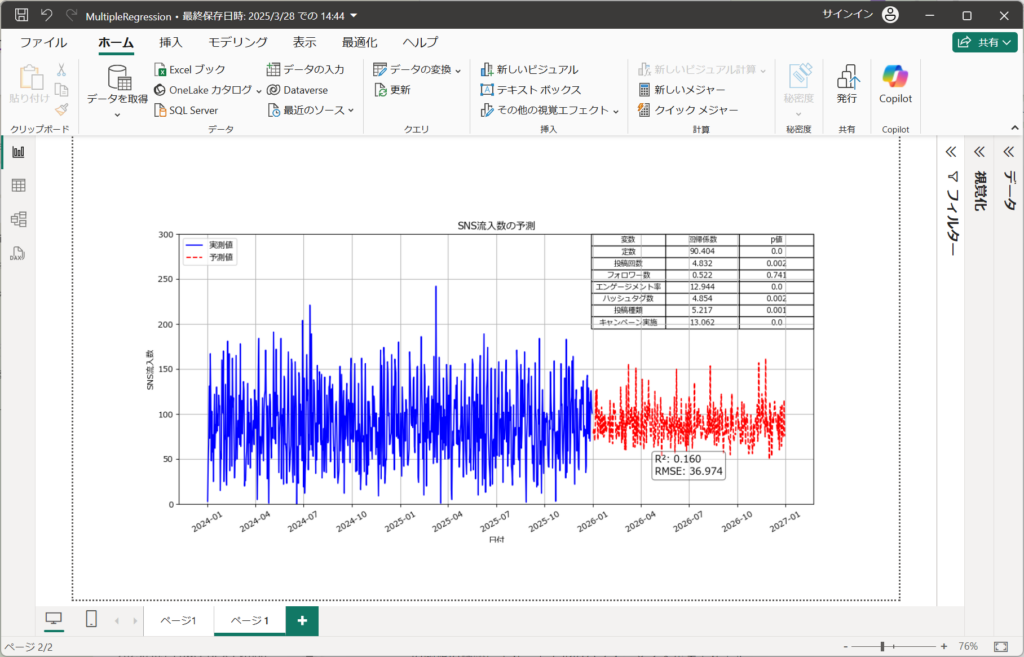
最後に重回帰分析のグラフを読み解きましょう。
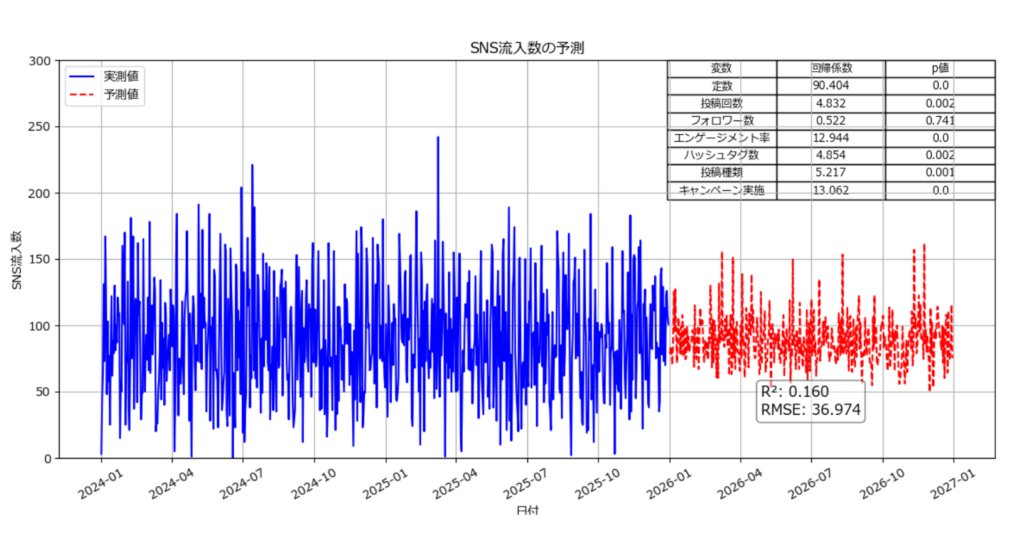
決定係数が0.160という値はかなり低いため、このモデルは目的変数の変動を十分に説明できていない可能性がある。つまり、「この重回帰モデルは説明変数を用いても、目的変数の大部分の変動を説明できていない」と解釈できる。
残りの84%(1 - 0.160)の変動は、説明変数以外の要因によって決まっていることを示唆する。
RMSE(36.974)について誤差が大きい可能性がある。例えば、目的変数が「SNS流入量」であるため、このモデルの予測は平均して±36.974の誤差を持つことになる。RMSEの絶対値だけでは「このモデルが良いのか悪いのか」は判断しづらいため、単独で利用せずに他の評価と合わせて活用する。
回帰係数・p値を一覧化すると以下となる。
| 変数名 | 回帰係数 | 解釈 |
|---|---|---|
| 投稿回数 | 4.832 | 投稿回数が1増えると、目的変数が4.832増加する。 |
| フォロワー数 | 0.522 | フォロワー数が1増えると、目的変数が0.522増加する(影響が小さい)。 |
| エンゲージメント率 | 12.944 | エンゲージメント率が1%増えると、目的変数が12.944増加する。最も影響が大きい。 |
| ハッシュタグ数 | 4.854 | ハッシュタグ数が1増えると、目的変数が4.854増加する。 |
| 投稿種類 | 5.217 | 投稿の種類が変わると、目的変数が5.217増加する。 |
| キャンペーン実施 | 13.062 | キャンペーンを実施すると、目的変数が13.062増加する。 |
| 変数名 | p値 | 有意性の評価 |
|---|---|---|
| 投稿回数 | 0.002 | 有意(影響あり) |
| フォロワー数 | 0.741 | 有意でない(影響がない可能性) |
| エンゲージメント率 | 0 | 有意(影響あり) |
| ハッシュタグ数 | 0.002 | 有意(影響あり) |
| 投稿種類 | 0.001 | 有意(影響あり) |
| キャンペーン実施 | 0 | 有意(影響あり) |
フォロワー数のp値が0.741と高く、統計的に有意ではない。つまり、フォロワー数を増やしても目的変数(おそらくエンゲージメントや売上)には有意な影響を与えない可能性がある。変数として削除を検討してもよい。他の変数(投稿回数、エンゲージメント率、ハッシュタグ数、投稿種類、キャンペーン実施)はp値が0.05未満であり、統計的に有意な影響があると判断できる。
以上のことから、決定係数・p値の結果より、特徴量(変数名)の削減を行い、決定係数・RMSEの改善がみられるか確認する。他にも有効化特徴量が無いか検討、不要な特徴量は削除するなどして、モデルの改善を図ることが求められる。
補足)
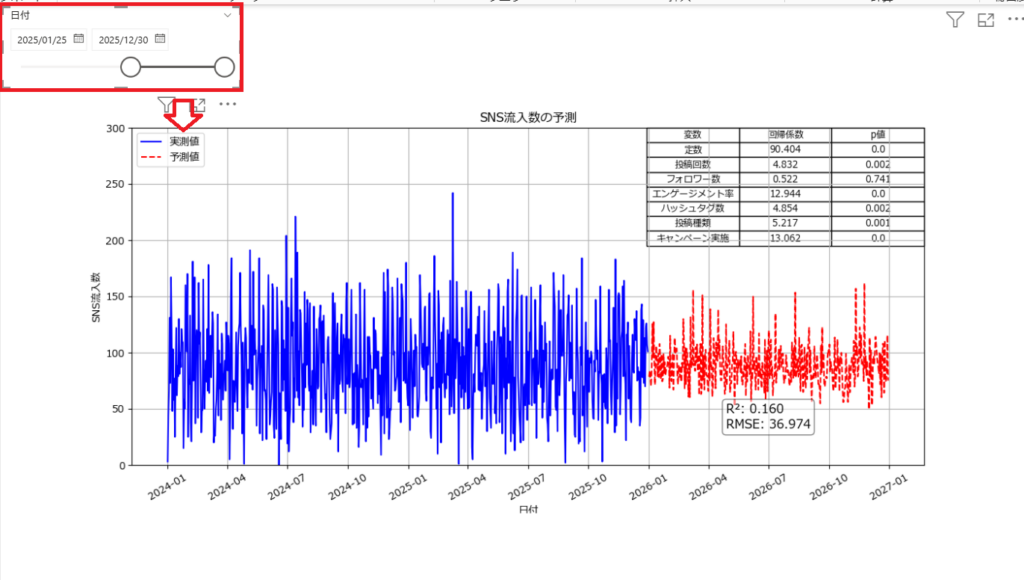
話が少しずれてしまいますが、Power BIのスライサーを追加設定しても、Python ビジュアルは変化しない。また、マウスオーバーしても、数値が表示されないので、標準のビジュアル機能(スライサーなど)がPythonビジュアルへ影響を及ぼすことができない。そのため、ダイナミックにビジュアルを操作したい場合、標準のビジュアルを用いる方が良いです。
まとめ(結論と今後の展望)
本記事では、重回帰分析を用いて、その精度を高めるために必要な取り組みについて説明しました。まず、データの前処理として標準化を実施し、モデルの精度向上の基盤を整えました。次に、回帰分析の結果をもとに、決定係数や誤差指標を用いてモデルの適合度を評価するとともに、各変数の影響度を分析し、統計的に有意な変数とそうでない変数を判別しました。その結果、精度向上に向けた改善点を明確にしました。
本記事の内容を参考にして、実践的なモデルの構築に生かしていただけますと幸いです。
