はじめに
「Power BI × Pythonで学ぶ主成分分析の実践」で作成した主成分分析(PCA)について解説します。PCAを実施したものの、結果の読み解き方がわからない方に向けて、詳しく説明します。
方法(アプローチ・使用技術)
前回のおさらい
エンゲージメントサーベイ結果からPCAを行い、散布図でビジュアルを作成しました。PCAと合わせてK-meansクラスタリングの作成まで完了しています。本記事はPCA分析の読み解き方から始めます。
PCAの読み方
PCAはPC1(第一主成分)とPC2(第二主成分)で構成されています。まずはPC1とPC2の説明をします。
PC1(第一主成分)とPC2(第二主成分)について
PC1(第一主成分)とは
データの分散を最大限に説明する軸(方向) である。
データのばらつき(分散)が最も大きい方向に設定される。
高次元空間において、データの情報を最もよく表す直線を求めるイメージ。
PC1の値が大きいほど、そのデータは第一主成分の方向に強く影響を受けている。
例:顧客の購買データにおいて、PC1が「購買金額の大きさ」や「購入頻度」と強く相関している場合、PC1が高いほど 優良顧客 である可能性が高い。
PC2(第二主成分)とは
PC1とは直交する(無相関な)軸であり、PC1の次にデータの分散をよく説明する方向 である。
PC1と直交する(90度の関係を持つ)ため、PC1とは異なる情報を表す。
PC2の寄与率(分散説明率)はPC1よりも低くなる(=PC1ほど重要ではない)。
PC1とPC2の2次元プロットを作ることで、データの構造を視覚的に把握しやすくなる。
例:PC2が「購買する商品の種類の多さ」と強く相関している場合、PC2が高いほど 多様な商品を購入する顧客 である可能性がある。
PC1とPC2を用いた解釈
PCAを使って次元削減したデータを PC1 と PC2 の散布図 で表現すると、クラスタの傾向が可視化しやすくなる。
プロット例
PC1(横軸):購買金額の大きさ
PC2(縦軸):購入する商品の種類の多様性
| PC1 | PC2 | 解釈 |
|---|---|---|
| 高 | 高 | 高額かつ多様な商品を買う顧客 |
| 高 | 低 | 高額な商品を買うが種類は少ない |
| 低 | 高 | 少額だが多様な商品を買う |
| 低 | 低 | 少額かつ購入の種類も少ない |
PC1、PC2の説明を決めるポイント
PC1の説明を適切に決めるには、以下のような手順を踏むのが有効です。
主成分負荷量(components)
主成分分析(PCA)の主成分負荷量(components)は、各変数が主成分にどれだけ寄与しているかを示す重要な指標。負荷量の値は、主成分に対する各変数の寄与度を示し、-1 から 1 の範囲で表される。この範囲で、各スコア(変数)の強弱を判断することが可能である。
主成分負荷量の解釈
0に近い値:その変数は主成分にほとんど寄与していない。
±0.3 ~ ±0.5:中程度の寄与。主成分に一定の影響を与えるが、他の変数にも影響される可能性がある。
±0.5 ~ ±0.7:比較的強い寄与。主成分に重要な影響を与えている。
±0.7 ~ ±1:非常に強い寄与。その変数は主成分の特徴を強く反映している。
※マイナスの負荷量は、その変数が主成分に対して 逆方向に寄与している ことを意味します。つまり、その変数の値が大きい(高い)ほど、主成分の値は逆方向に変化します。具体的には、その変数が高い場合、主成分の値は低くなる傾向があるということです。
具体的な例
もし、あなたのPCA結果で以下のような主成分負荷量が得られたとします。
| 変数 | PC1負荷量 |
|---|---|
| 継続意向 | 0.65 |
| やりがい | 0.8 |
| 職場環境 | 0.45 |
| 人間関係 | 0.3 |
| 成長・キャリア | 0.6 |
| 評価・承認 | 0.5 |
この場合、PC1に対するスコア群の強弱を以下のように解釈できます
・やりがい(0.80)、継続意向(0.65)、成長・キャリア(0.60) は強い寄与(±0.5以上)を持ち、PC1に大きな影響を与えている。
・ 評価・承認(0.50)と職場環境(0.45) は中程度の寄与(±0.3~0.5)を持ち、PC1にある程度影響を与えているが、強い影響ではない。
・人間関係(0.30) はPC1にあまり影響を与えていない。
このように、負荷量の値を基にスコア群の影響の強さを評価することで、主成分の意味をより明確に説明することができます。
これらのパターンを見て、共通する概念を探すことで、PCAの価値が発揮されます。
では、実際に見てみます。
主成分負荷量を読み解く
「Pythonスクリプトを実行する」のステップにて、「components」を展開します。
展開された結果から、PC1とPC2の主成分負荷量が表示されます。
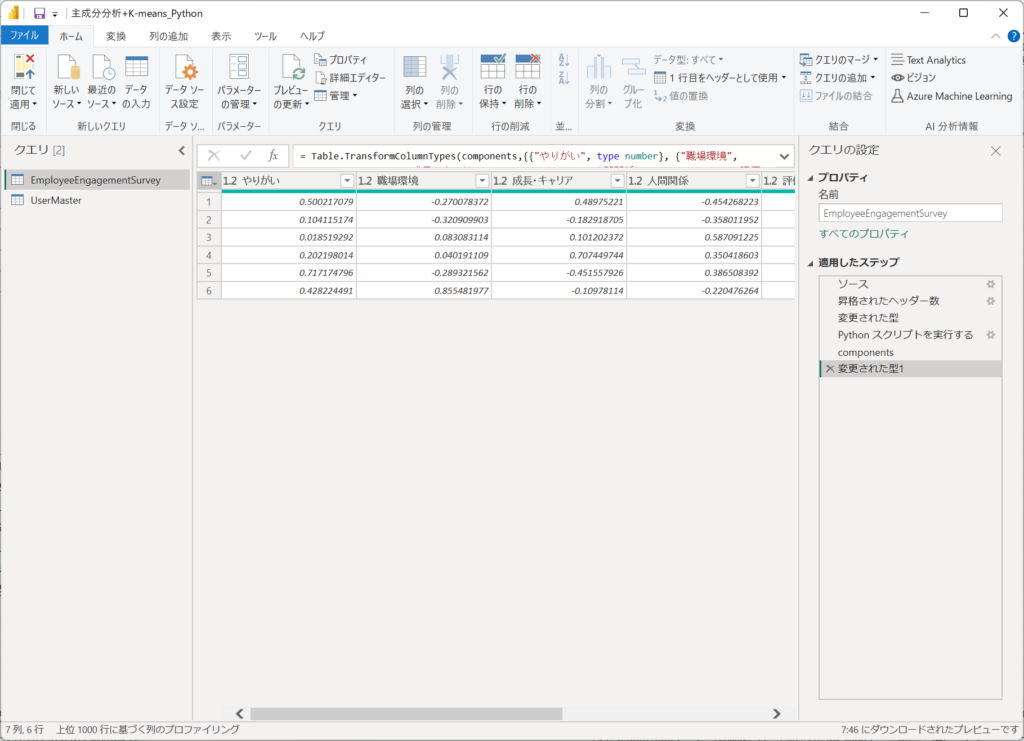
| やりがい | 職場環境 | 成長・キャリア | 人間関係 | 評価・承認 | 継続意向 | PC No. |
|---|---|---|---|---|---|---|
| 0.500217 | -0.270078 | 0.48975221 | -0.454268 | 0.445758 | -0.178671 | 1 |
| 0.104115 | -0.32091 | -0.182918705 | -0.358012 | -0.138509 | 0.839857 | 2 |
| 0.018519 | 0.083083 | 0.101202372 | 0.587091 | 0.682749 | 0.414355 | 3 |
| 0.202198 | 0.040191 | 0.707449744 | 0.350419 | -0.540715 | 0.204572 | 4 |
| 0.717175 | -0.289322 | -0.451557926 | 0.386508 | -0.153555 | -0.158369 | 5 |
| 0.428224 | 0.855482 | -0.10978114 | -0.220476 | -0.004067 | 0.155229 | 6 |
PC1は、以下の解釈となる。
・やりがい(0.50)は強い寄与(±0.5以上)を持ち、PC1に大きな影響を与えている。
・成長・キャリア(0.48)、人間関係(-0.45)、評価・承認(0.44) は中程度の寄与(±0.3~0.5)を持ち、PC1にある程度影響を与えているが、強い影響ではない。
・職場環境(-0.27) と継続意向(-0.17) は、PC1にあまり影響を与えていない。
PC2は、継続意向が0.83と高いため、今後も自社に勤めていきたいかを強く表している。

ここで気になる点として、表にはPCが1~6の計6つ存在しています。
PC3~6は考慮しなくてよいか?と気になる方も多いと思います。
そこで確認すべき点は、各主成分がデータの分散をどの程度説明するかを示す 「分散説明率」です。
分散説明率を読み解く
「Pythonスクリプトを実行する」のステップにて、「evr」を展開します。
展開された結果から、PC1~PC6の分散説明率が表示されます。
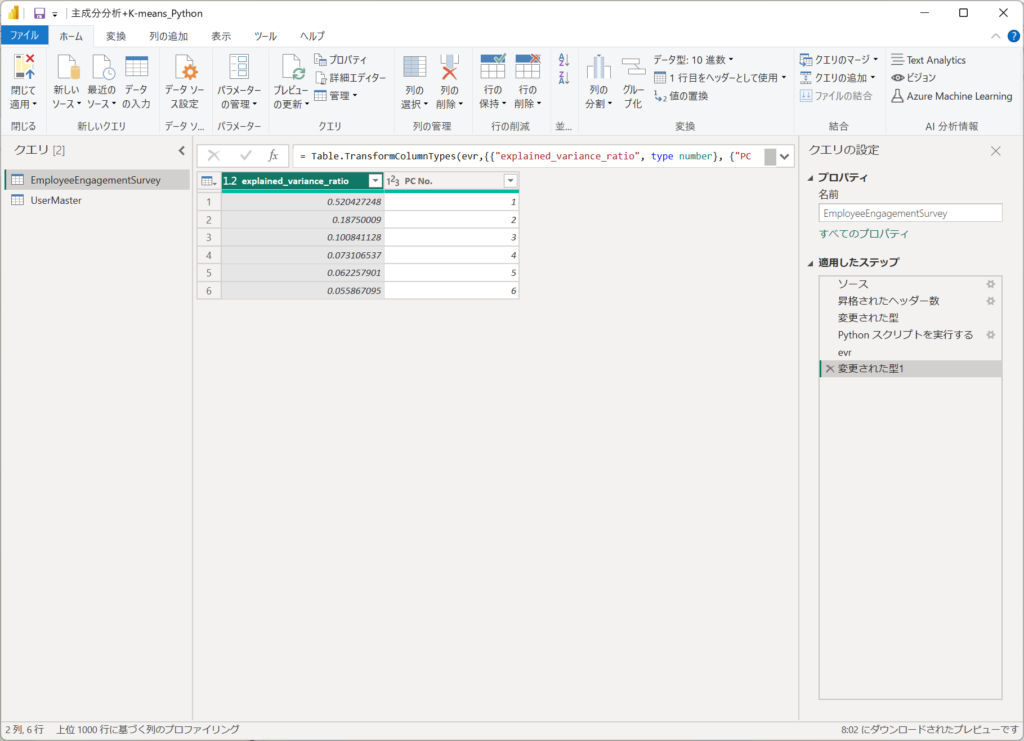
| explained_variance_ratio | PC No. |
|---|---|
| 0.520427248 | 1 |
| 0.18750009 | 2 |
| 0.100841128 | 3 |
| 0.073106537 | 4 |
| 0.062257901 | 5 |
| 0.055867095 | 6 |
全体のうちPC1が寄与している割合は、52%、PC2が18%、PC3以降は10%以下を表しています。
PC1とPC2を足しあわせると、累積の寄与している割合が70%となり、凡そをカバーできていると理科することができます。
そのため、PC3以降は与える影響が少ないため、PC1とPC2のみを見ています。
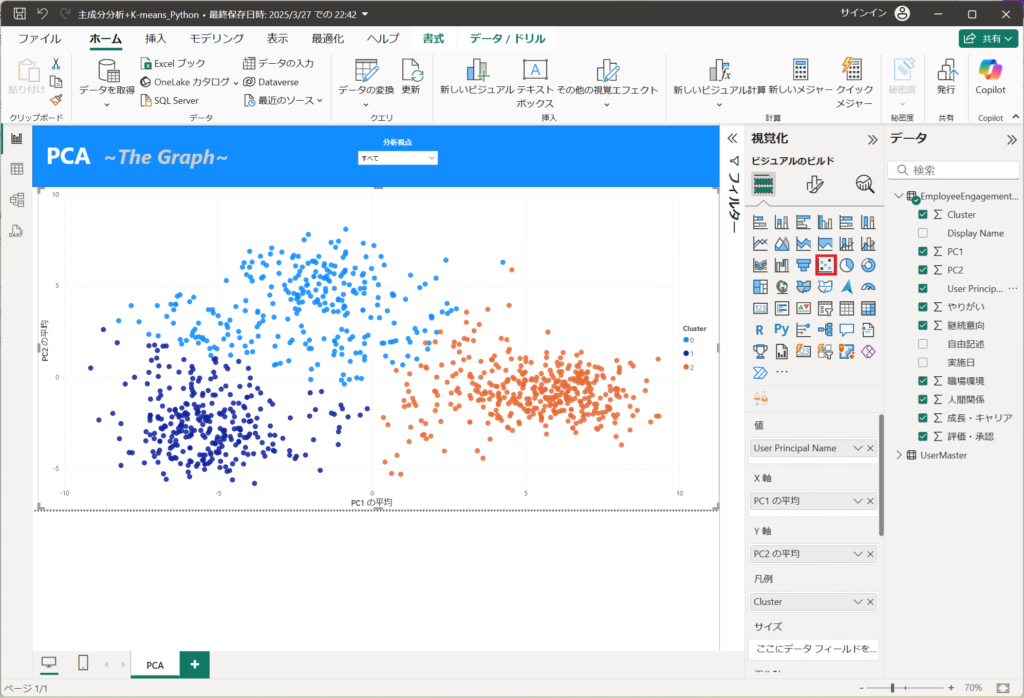
最後にPCAのグラフを読み解きましょう。
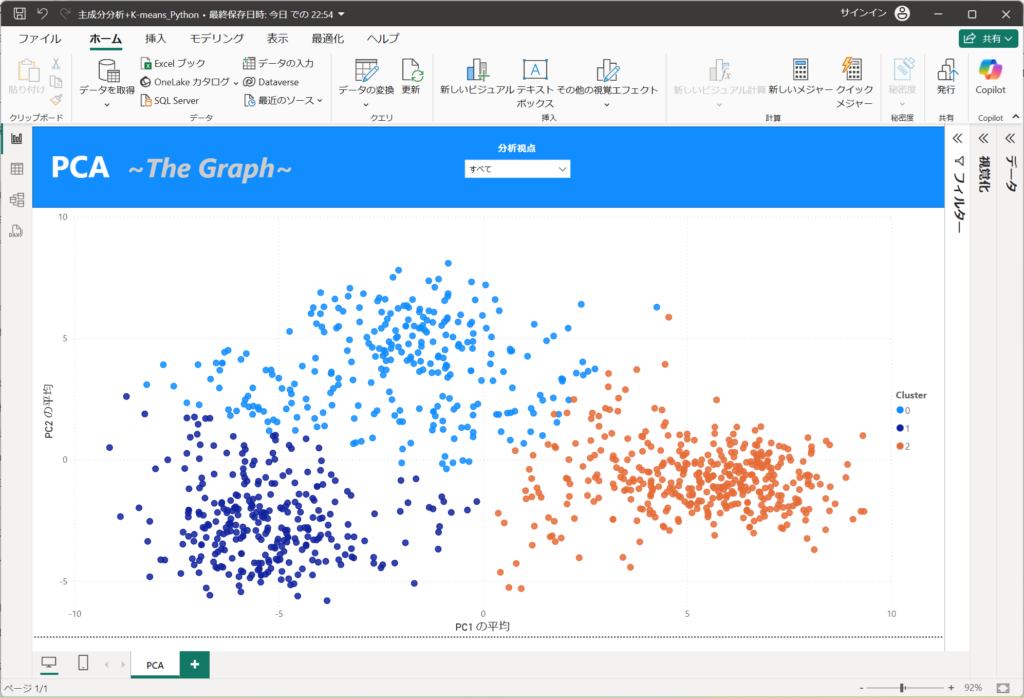
PC1はやりがいが最も影響を与えており、成長・キャリア、評価、承認の割合が高い傾向にあります。
そのため、内発的動機をもって、仕事へのやりがいを感じており、成長・キャリアのスコアが高い人の傾向を表しています。人間関係は少ないほうが良いと感じている人が多いのでしょう。
PC2は継続勤務が高いため、離職したいかどうかを表します。
このことから、K-meansのClusterが
青色は離職率が低く、適度にやりがいをもって働いているクラスターを指します。
オレンジは、仕事に対してやりがいをもち、成長・キャリア、評価、承認が高いクラスターです。しかし、離職の可能性があるため、注意が必要です。
紺色は、エンゲージが低い層です。なるべく、注意して見守るべき集合です。
PCAとK-meansクラスタリングを使ってエンゲージメントサーベイスコアを見ることで様々なことがわかります。
非常に興味深い分析になると思います。
まとめ(結論と今後の展望)
本記事では、Power BIとPythonを用いた主成分分析(PCA)を解説しました。Power BIは可視化をすることがGOALではありません。可視化した先のインサイトまで見出すことまでがGOALです。PCAは一見難しそうに思えますが、実際に触ってみると難しくありません。ぜひとも実務にてPower BIとPythonの連携を活用したPCA分析を行い、より効果的なデータ活用を目指してみてください。
