Power BI × Pythonで学ぶ主成分分析の実践

1 概要（目的・背景）
2 読み手（誰に向けた記事か？）
3 ブログの目標設定（具体的な目標）
4 方法（アプローチ・使用技術）
5 まとめ（結論と今後の展望）

概要（目的・背景）

現代のビジネス環境では、膨大なデータを効率的に分析し、意思決定に活用することが求められています。しかし、多くの変数を持つデータセットは複雑で、全体像を把握するのが難しい場合があります。例えば、マーケティング部門が顧客の購買行動を分析する際、年齢、収入、購買履歴、ウェブサイトの閲覧履歴など、多数の変数が関与します。これらのデータを効果的に分析し、視覚化するためには、次元削減の手法が有用です。
主成分分析（PCA）は、データの次元を削減し、主要な情報を抽出する統計手法です。これにより、複雑なデータをシンプルにし、視覚化や解析を容易にします。本記事では、Power BIとPythonを組み合わせて、PCAを実践する方法を解説します。これにより、データ分析の効率と精度を向上させることを目指します。

読み手（誰に向けた記事か？）

本記事は、Power BIにてデータ分析に興味があるデータサイエンティストを対象としています。主成分分析（PCA）の概念から実践的な実装方法までを理解し、日々の業務やプロジェクトに応用できるようになることを目指しています。

ブログの目標設定（具体的な目標）

本記事の目標は、以下の通りです。
・PCAの基本概念とその必要性を理解する
　PCAがどのような手法であり、なぜデータ分析において重要なのかを明確にします。
・PCAのメリットとデメリットを把握する
　PCAを適用する際の利点と注意点を理解し、適切な場面で活用できるようにします。
・Power BIとPythonを用いたPCAの実践方法を習得する
　具体的な手順を通じて、実際のデータセットにPCAを適用し、結果を解釈するスキルを身につけます。
これらの目標を達成することで、読者はPCAを効果的に活用し、複雑なデータセットから有益な洞察を得る能力を向上させることができます。

方法（アプローチ・使用技術）

主成分分析（PCA）とは？

主成分分析（PCA）は、多変量データの次元を削減し、データの本質的な構造を明らかにする統計手法です。多数の変数を持つデータセットを、情報の損失を最小限に抑えつつ、より少ない数の新しい変数（主成分）に変換します。これにより、データの可視化や解釈が容易になり、分析の効率が向上します。

なぜPCAが必要なのか？

データ分析において、多くの特徴（変数）を持つデータは理解しにくく、計算負荷も高くなります。例えば、マーケティング分析では顧客の年齢、収入、購買履歴、ウェブ閲覧履歴など多くのデータを扱いますが、これらすべてを同時に考慮するのは難しいことがあります。PCAを使うことで、データの本質的な情報を損なわずに、次元を減らしてシンプルにすることができます。

PCAの仕組み

PCAは、元のデータの変数同士の関係を分析し、互いに相関の強い情報を統合し、新しい変数（主成分）を作り出します。

データの標準化: PCAを適用する前に、すべての変数を同じ尺度にそろえるために標準化を行います（平均を0、分散を1にする）。
共分散行列の計算: データの各変数同士の関係（どの程度影響を与えているか）を分析します。
固有値・固有ベクトルの計算: データのばらつきを説明する主成分を求めます。
主成分の選択: ばらつきを最もよく説明する主成分を選び、新しい座標軸としてデータを再構成します。

例えば、身長と体重のデータがある場合、PCAを適用すると「全体の体格を示す指標」として第1主成分が得られるかもしれません。このように、複数の変数をまとめ、データの要点をより少ない次元で表現できます。
ここまでで仕組みを説明しましたが、すべて理解する必要は無いです。これらの仕組みをPythonがすでに用意したライブラリを用いて、一括で処理するため、概要を理解するのみで十分です。

PCAのメリット

データの可視化と解析の容易化：高次元のデータを2次元や3次元に縮約することで、グラフなどを用いた視覚的な解析が可能になります。これにより、データのパターンや傾向を直感的に把握できます。
ノイズの除去：PCAは、データの中で重要ではない（分散が小さい）成分を除外するため、ノイズを削減し、データの本質的な部分を抽出できます。これにより、分析の精度が向上する場合があります。
相関の把握：PCAは、元の変数同士の相関関係を主成分に集約します。これにより、データの潜在的な構造やパターンを明らかにし、多重共線性の問題を軽減できます。

PCAのデメリット

解釈の難しさ：PCAによって得られる主成分は、元の変数が線形結合された新しい変数であるため、その意味を解釈するのが難しい場合があります。特に、ビジネス上の意思決定において、具体的な変数の影響を知りたい場合には不向きです。
情報の損失：次元削減を行う際、データの一部の情報が失われる可能性があります。特に、少数の主成分でデータを表現する場合、元のデータが持っていた詳細な情報が削減され、分析の精度が低下するリスクがあります。

PCAの設定手順

【前提】
Power BIのPowerQueryを用いてPCAを作成します。PCAの設定を完了したPower BIファイルは下記の添付ファイルです。必要な設定はすべて完了していますので、添付ファイルをベースにPCAの設定方法を説明していきます。

: 素材＠Power BI × Pythonで学ぶ主成分分析
はじめに本記事は、「Power BI × Pythonで学ぶ主成分分析の実践」にて作成したPower BI ファイル（.pbixファイル）を共有するものです。 https://28samon.com ...

今回用意しているデータは、エンゲージメントサーベイの結果をPCAで整理します。エンゲージメントは、「やりがい」、「人間関係」、「職場環境」など変数が多く、傾向が読み取り辛いです。そのため、PCAの次元削除を用いて、全体の傾向を把握しやすくすることを目的とします。

1.「主成分分析+K-means_Python.pbix」をダブルクリックして開く。

2.「ホーム」タブから「データの変換」ボタンを押下する。

3.左メニューより「EmployeeEngagementSurvey」を選択する。
※EmployeeEngagementSurveyにPCAの設定を行っています。

Niwa

PowerQueryは３つで構成されています。
各ステップを説明していきます。
①.エンゲージメントサーベイのCSV取得
②.取り込んでデータに対してPythonにてPCAを実施
③.PCAの結果をテーブルへ展開

4.「ソース、昇格されたヘッダー数、変更された型」は①エンゲージメントサーベイのCSV取得の処理です。

Power BIへCSVを取り込むときに自動で設定される定義です。"データ分析の第１歩 ~データ取り込みの基礎知識➊~（Day1）"で行っているCSV取り込み処理と同じ手順であるため、詳細な説明は下記のリンク先を参照してください。

: データ分析の第１歩 ~データ取り込みの基礎知識➊~（Day1）
はじめに Power BI Desktopは、ビジュアライゼーションとレポート作成のための強力なツールです。しかし、使い方が分からない、使い始めるための適切なデータが手元にない、といった理由でPowe ...

5.「Python」本記事のメインとなる「PCA」のコードが定義されたステップです。

Power QueryでPythonを実行する手順を詳細に説明します。
①.Pythonのステップを入れるときは「変換」タブから「Pythonスクリプトを実行する」ボタンを押下する。

②.Pythonスクリプトを実行する、コード入力ウィンドウが立ち上がります。
画面中央のスクリプトへPythonのコードを入力します。

③.以下のコードを入力する。

# 'dataset' はこのスクリプトの入力データを保持しています
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans

# 数値データのみを抽出（PCA用）
numeric_dataset = dataset.select_dtypes(include=[np.number])

# PCAの適用
X = numeric_dataset.values
pca = PCA()
pca.fit(X)
pca_point = pca.transform(X)

dataset['PC1'] = pca_point[:, 0]
dataset['PC2'] = pca_point[:, 1]

# 主成分の分散説明率
evr = pd.DataFrame({'explained_variance_ratio': pca.explained_variance_ratio_}) 
evr['PC No.'] = evr.index + 1

# 主成分の係数
components = pd.DataFrame(pca.components_, columns=numeric_dataset.columns)
components['PC No.'] = components.index + 1

# K-means クラスタリング
km = KMeans(n_clusters=3, init='random', n_init=10, max_iter=300, tol=1e-4, random_state=0)
y_km = km.fit_predict(pca_point)

dataset['Cluster'] = y_km

④.コードを順に説明します。

必要なライブラリをインポートする。

import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans

numpy：数値計算ライブラリ（PCAやK-meansで使用）
pandas：データ処理ライブラリ（データフレーム操作に使用）
sklearn.decomposition.PCA：主成分分析（PCA）を行うためのライブラリ
sklearn.cluster.KMeans：K-means クラスタリングを行うためのライブラリ

数値データの抽出

numeric_dataset = dataset.select_dtypes(include=[np.number])

dataset はPower BIの入力データ（Pandasのデータフレーム）。
select_dtypes(include=[np.number]) により、数値型の列のみを抽出して numeric_dataset に格納。
PCAは数値データに対してのみ適用可能であるため、この前処理を実施。

PCAの適用

X = numeric_dataset.values
pca = PCA()
pca.fit(X)
pca_point = pca.transform(X)

numeric_dataset.values により、データフレームを NumPy配列（ndarray）に変換。
PCA() でPCAオブジェクトを作成。
pca.fit(X) により、データの主成分を学習（固有値・固有ベクトルを計算）。
pca.transform(X) により、元のデータを主成分空間に射影（次元圧縮）。
→ pca_point には主成分得点（主成分空間上の座標）が格納される。

第1主成分（PC1）、第2主成分（PC2）の追加

dataset['PC1'] = pca_point[:, 0]
dataset['PC2'] = pca_point[:, 1]

主成分分析によって得られたデータ pca_point の第1主成分（PC1）と第2主成分（PC2）を dataset に追加。
pca_point[:, 0] は PC1（第一主成分）の値。
pca_point[:, 1] は PC2（第二主成分）の値。
→ これにより、元のデータに次元削減後の情報が付加される。

主成分の分散説明率 ※グラフに利用しないが、後程解説のため算出

evr = pd.DataFrame({'explained_variance_ratio': pca.explained_variance_ratio_}) 
evr['PC No.'] = evr.index + 1

pca.explained_variance_ratio_ は、各主成分がデータの分散をどの程度説明するかを示す分散説明率。
evr は、PC1, PC2, ... の各主成分の分散説明率をデータフレーム形式で格納。
evr['PC No.'] = evr.index + 1 により、各主成分に PC番号（1, 2, 3,...）を追加。

主成分の係数（固有ベクトル）※グラフに利用しないが、後程解説のため算出

components = pd.DataFrame(pca.components_, columns=numeric_dataset.columns)
components['PC No.'] = components.index + 1

pca.components_ は、各主成分の係数（固有ベクトル）。
係数は、元の特徴量がどの程度各主成分に寄与しているかを示す。
components データフレームには、各主成分（PC1, PC2, ...）の元の変数ごとの寄与度が格納される。

K-meansクラスタリング

km = KMeans(n_clusters=3, init='random', n_init=10, max_iter=300, tol=1e-4, random_state=0)
y_km = km.fit_predict(pca_point)
KMeans(n_clusters=3, init='random', n_init=10, max_iter=300, tol=1e-4, random_state=0)：

n_clusters=3 → クラスター数を 3つに設定。
init='random' → 初期クラスタ中心をランダムに設定。
n_init=10 → 10回異なる初期値で試行し、最良の結果を採用。
max_iter=300 → 最大反復回数を 300回に設定。
tol=1e-4 → 収束判定の許容誤差。
random_state=0 → 再現性を確保するための乱数固定。
fit_predict(pca_point) により、主成分空間上でクラスタリングを実行し、各データにクラスタラベル（0,1,2）を割り当てる。

クラスター情報の追加

dataset['Cluster'] = y_km

クラスター番号（0, 1, 2）を dataset に追加。
dataset は、元のデータに主成分（PC1, PC2）とクラスタラベルが追加された形となる。
PCA分析に加えて、K-meansクラスタリングで３つのクラスタを凡例で把握できるようにしています。

6.「Pythonスクリプトで実行する」の結果から、「dataset」を展開すると、ステップに「dataset」と「変更された型1」が自動生成されます。

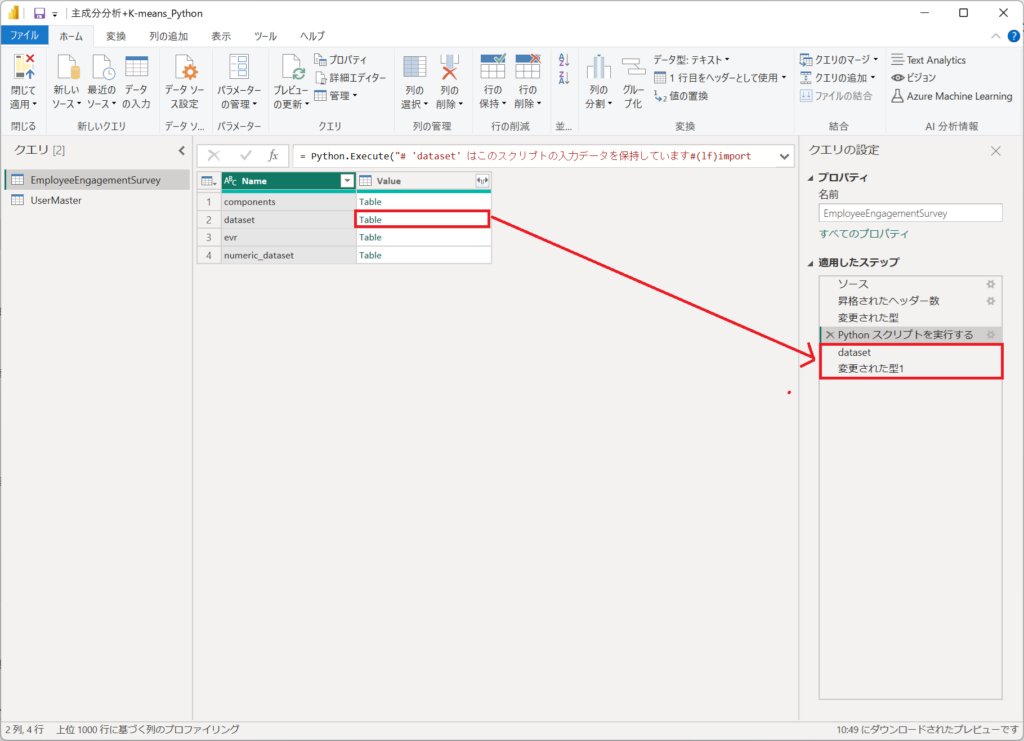
datasetに第1主成分（PC1）、第2主成分（PC2）、l-meansのクラスター情報が格納されています。
ここまででPowerQueryの設定は終了です。

7.ビジュアルから散布図を選択する。
散布図を選択した後、以下の値を設定する。
値：User Principal Name
X軸：PC1 の平均
Y軸：PC2 の平均
凡例：Cluster
ヒント：継続意向の合計、やりがいの合計、職場環境の合計、人間関係の合計、成長・キャリアの合計、評価・承認の合計

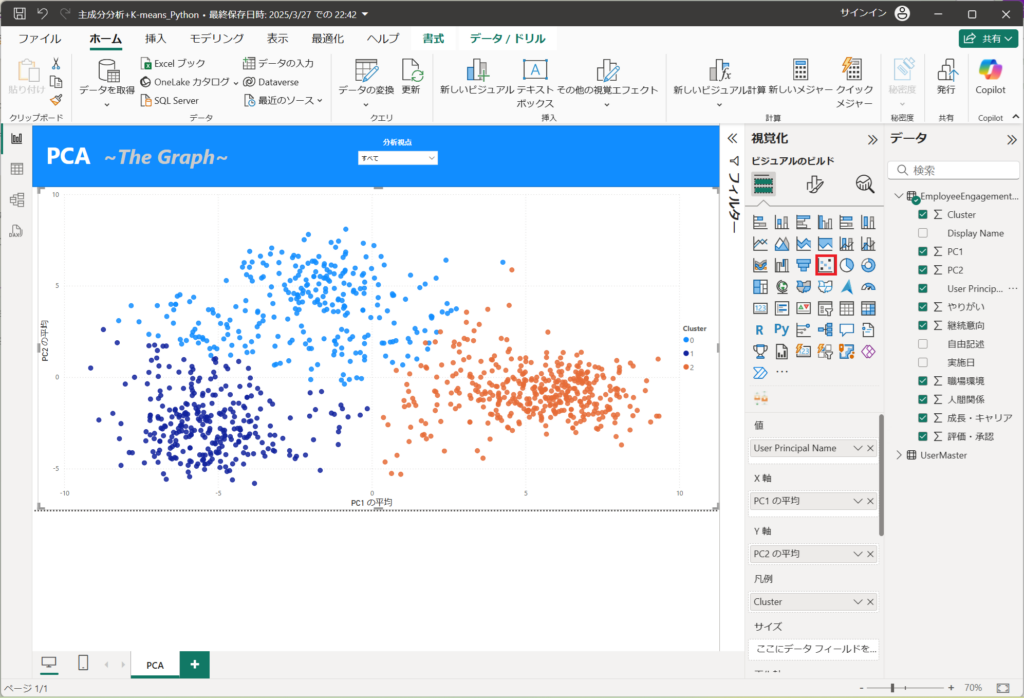
以上でPCAの可視化まで完了しました。
PCAとK-meansクラスタリングで全体の傾向が見えるようになりました。
引き続き、グラフの読み方を解説します。

: Power BI × Pythonで学ぶ主成分分析の解説
はじめに「Power BI × Pythonで学ぶ主成分分析の実践」で作成した主成分分析（PCA）について解説します。PCAを実施したものの、結果の読み解き方がわからない方に向けて、詳しく説明します ...

まとめ（結論と今後の展望）

本記事では、Power BIとPythonを用いた主成分分析（PCA）の実践方法を解説しました。PCAを活用することで、複雑なデータをシンプルにし、視覚的な洞察を得やすくなります。Power BIとPythonの連携を活用し、より効果的なデータ活用を目指してみてください。