本記事では、確率変数の取りうる値の種類に基づき、「離散型」確率分布と「連続型」確率分布という2つの分布のタイプについて解説します。なお、本文中では読みやすさのため、離散型確率分布を「離散分布」、連続型確率分布を「連続分布」と略記します。
とびとび型となめらか型とは?
統計学における基本的な概念のひとつに、「確率分布」があります。この確率分布は、確率変数がどのような値をとり、それぞれの値にどの程度の確率が割り当てられているかを示すものです。確率分布には大きく分けて、「とびとび型」と「なめらか型」の2種類があります。これらの違いを理解することは、統計モデルの選択や機械学習アルゴリズムの活用にも直結する重要なポイントです。
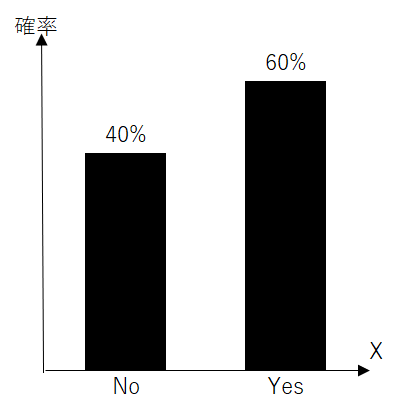
まず、とびとび型とは、とは、確率変数がとりうる値が数えられる場合の「離散分布」を指します。たとえば、サイコロの出目(1〜6)や、Yes・No(二値)などが該当します。代表的な離散分布には、二項分布やベルヌーイ分布などがあります。
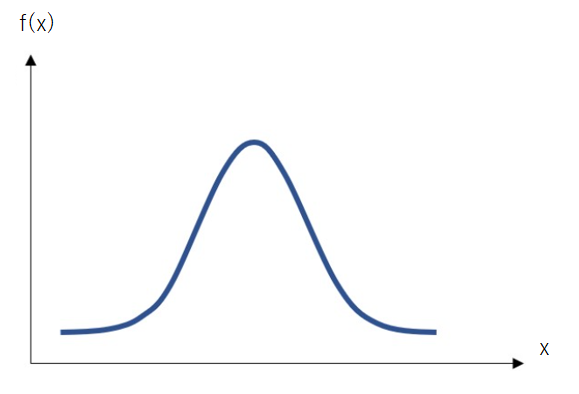
一方、なめらか型は、確率変数が連続的な範囲の値をとる場合に用いられる「連続分布」をさします。たとえば、身長や体重、温度など、任意の実数値をとる量が該当します。連続分布では、ある特定の値をとる確率はゼロと考え、代わりにある範囲に含まれる確率を議論します。代表的な連続分布には、正規分布や一様分布などがあります。
この違いをしっかりと理解する場合、本ブログサイトの「重回帰分析」や「ロジスティック回帰」といったモデルにて理解が深まります。
✅重回帰分析では目的変数が連続値(例:売上金額)であるため、正規分布などの連続分布に基づいた前提が使われます。
✅一方、ロジスティック回帰では目的変数が0または1の離散値(二値)であるため、離散的な分布モデルが背景にあります。
このように、対象とするデータが離散なのか連続なのかによって、選択すべき分析手法や前提とする分布の形が大きく変わるのです。
なぜ離散分布と連続分布が重要なのか?
離散分布と連続分布を正しく区別できるようになることは、統計学を正しく使いこなす上で非常に重要です。なぜなら、データの性質に応じた適切な分析手法を選ぶことが、結論の妥当性を左右するからです。
例えば、商品の購入有無(はい/いいえ)を予測するために、誤って重回帰分析(連続値を対象とした手法)を用いると、結果として0.7や-0.3といった理解が難しい予測値が出力されてしまいます。こうした事態を避けるには、目的変数が0または1の離散値をとることを前提に設計されたロジスティック回帰を選ぶべきです。
また、データの分布特性に基づく仮定は、統計的推定や仮説検定の際にも大きな影響を及ぼします。例えば正規分布を仮定するt検定は、連続分布の前提があるからこそ成り立つ方法です。一方、ポアソン分布を仮定したモデルは、ある時間内に発生する出来事の回数(例:コールセンターへの電話件数)などの離散的なデータに適用されます。
さらに、近年の機械学習においても、「分類」と「回帰」という2つのタスクに分けて考える必要があります。分類タスクでは出力がラベル(離散値)であり、回帰タスクでは出力が数値(連続値)です。このように、離散と連続の違いは、AIの設計にまで関わってくるのです。
つまり、データ分析や統計モデリングを行う際に、「これは離散か?連続か?」という問いに答えることは、分析の出発点であり、非常に重要なステップであるといえます。
学びを深めるためのポイント
1.変数の種類を明確に分類すること
自分が扱っている(あるいは扱いたい)データの「変数の種類」を明確に分類することが出発点です。変数が数値かカテゴリか、また数値であっても測定単位や意味に着目し、「本当に連続的な変数か」を問い直すことが重要です。たとえば、1〜5の満足度評価は一見数値に見えますが、実は順序尺度に近い性質を持つ離散値であることが多いため、分析方法の選択には注意が必要です。
| 尺度の種類 | 例 | |
|---|---|---|
| 質的変数 (数値では無いデータ) | 名義尺度 (値の間に順序や大小関係がない) | 性別、名前 |
| 順序尺度 (値の間に順序あり、間隔の「差」が等しいとは限らない) | 顧客満足度、ランキング | |
| 量的変数 (数値データ) | 間隔尺度 (数値の間隔(差)が等しく意味を持つが、「0=無」が存在しない) ※0度は"温度がない"という意味ではなく、相対的な温度として0度であることを指す | 気温(摂氏)、時刻 |
| 比例尺度 (「0=無」があり、加減乗除すべての計算が意味を持つ) ※売上額が0円の場合、売上"無し"を指す。 | 売上、体重、年齢 |
尺度の違いを一言で表すと以下の表です。
| 尺度 | 順序 | 間隔 | 絶対0 |
|---|---|---|---|
| 名義尺度 | ✕ | ✕ | ✕ |
| 順序尺度 | 〇 | ✕ | ✕ |
| 間隔尺度 | 〇 | 〇 | ✕ |
| 比例尺度 | 〇 | 〇 | 〇 |
2.実際のビジネス課題と結びつけて考える
教科書的な知識だけでなく、実際のビジネス課題と結びつけて考えることが重要です。たとえば「ユーザーが次回も購入するか否か」という課題は離散的な予測であり、連続的な「客単価予測」とは異なるモデリングが必要になります。こうした区別は、すべてのビジネスパーソンにとっても有益なリテラシーとなります。
まとめ
本記事では、統計学における基礎概念である「離散分布」と「連続分布」について解説しました。離散分布とは数えられる値をとる確率変数に関する分布であり、サイコロの目や購入有無などが代表例です。一方、連続分布は実数として連続的な値をとる変数に対応しており、身長や気温などの変数が当てはまります。
これらの違いは、データ分析の手法選定に直結します。特に、重回帰分析のように連続的な目的変数を扱う手法と、ロジスティック回帰のように離散的な目的変数を扱う手法とでは、適用される前提や仮定が大きく異なります。そのため、分析に入る前に「このデータはどの分布を前提とすべきか?」を見極める力が求められます。また、実務においては、データの可視化や分析ツールを使いこなすだけでなく、変数の性質に基づいたモデル選択の力が問われます。離散分布と連続分布を見分け、適切な分布を仮定してモデルを構築する力は、すべての分析者に求められる基礎的かつ実践的なスキルです。
このように、分布の種類を理解し、使いこなすことは、統計学の基礎を固めるだけでなく、ロジスティック回帰や重回帰分析といった応用手法への道を拓くものです。これを機に、データの「顔」をよく見て、統計学の基盤をさらに深めていきましょう。