目次
概要(目的・背景)
ビジネスの現場では、売上予測や顧客行動の理解など、多くの場面で複数の要因が絡み合っています。例えば、あるカフェチェーンが新店舗を出店する際、席数、最寄駅からの距離、モーニングサービスの有無など、さまざまな要素が売上に影響を与えると考えられます。こうした複数の要因と結果の関係性を明らかにする手法が「重回帰分析」です。
本記事では、重回帰分析の基本的な概念から、Power BIとPythonを用いた実践的な分析手法までを詳しく解説します。データ分析をこれから始める方や、既に取り組んでいるがさらにスキルを向上させたいと考えている方々にとって、有益な内容となることを目指しています。
読み手(誰に向けた記事か?)
本記事は、Power BIを使い始めたデータアナリストは、基本的な操作には習熟しているものの、Pythonとの連携や統計的手法の導入を検討している方々や、Pythonに興味を持つエンジニアは、データ分析の領域に足を踏み入れ、ビジネスでの活用方法を模索している方々へ有益な情報を提供します。本記事を通じて、これらの読者の皆様が重回帰分析の概念を理解し、Power BIとPythonを活用した実践的な手法を身につけることを目指します。
ブログの目標設定(具体的な目標)
本記事の目標は、以下の通りです。
・重回帰分析の基本概念の理解
複数の説明変数と目的変数の関係性を明らかにする重回帰分析の概念を理解する。
・Power BIとPythonの連携方法の習得
Power BI内でPythonスクリプトを実行し、データ分析を行う手順を理解する。
これらの目標を達成することで、読者の皆さんはビジネスデータの分析力を向上させ、より精度の高い予測や意思決定を行うための基盤を築くことを目標とします。
方法(アプローチ・使用技術)
重回帰分析とは?
まず、重回帰分析の基本的な概念について説明します。重回帰分析は、複数の説明変数(独立変数)と1つの目的変数(従属変数)との関係性を数式で表す統計手法です。これにより、各説明変数が目的変数にどの程度影響を与えているかを定量的に評価できます。例えば、カフェチェーンの年間売上高を予測する際に、以下の要素が影響を与えると考えられます。
・席数:店舗内の座席数
・最寄駅からの徒歩時間:駅から店舗までの距離
・モーニングサービスの有無:朝食サービスの提供有無
これらの要素を説明変数とし、年間売上高を目的変数として重回帰分析を行うことで、各要素が売上に与える影響を数値化できます。
重回帰分析のメリット・デメリット
分析手法として重回帰分析を用いることで、以下のようなメリット・デメリットが考えられます。
メリット
・多要因の影響評価
→複数の要因が目的変数に与える影響を同時に評価できるため、現実の複雑な関係性をモデル化しやすい。
・予測精度の向上
→単回帰分析に比べ、多くの情報を考慮するため、予測の精度が向上する可能性がある。
デメリット
・過学習のリスク
→説明変数が多すぎると、モデルがデータに過度に適合し、新しいデータに対する予測精度が低下する可能性がある。
・多重共線性の問題
→説明変数同士が強く相関している場合、各変数の影響を正確に評価することが難しくなる。
重回帰分析の設定手順
【前提】
これまではPowerQueryへPythonを組み込んでデータ分析していましたが、今回はPower BIのビジュアルを用いて重回帰分析を作成します。重回帰分析の設定を完了したPower BIファイルは下記の添付ファイルです。必要な設定はすべて完了していますので、添付ファイルをベースに設定方法を説明していきます。
今回用意しているデータは、SNSのパフォーマンスを定量的に測定し、サイトへの流入数を予測するために、以下のデータを準備しています
※期間2024年1月~2025年12月末
・SNS流入数(PV) - SNSからWebサイトへの訪問数
・投稿回数(回/月) - 月に何回投稿を行ったか
・フォロワー数(人) - その月のフォロワーの総数
・エンゲージメント率(%) - いいね・コメント・シェアなどの合計 ÷ インプレッション数
・ハッシュタグの数(平均/投稿) - 1投稿あたりのハッシュタグの数
・投稿の種類(0: 画像, 1: 動画) - 画像と動画のどちらが効果的か
・キャンペーン実施(0: なし, 1: あり) - 特別なプロモーションがあったか
これらの情報を用いて、2026年1月~12月のサイト流入数を予測します。
1.「MultipleRegression.pbix」をダブルクリックして開く。
2.以下のメッセージが表示されます。「有効にする」を選択する。

3.画面中央のビジュアルを選択する。
Pythonスクリプト エディターが表示されることを確認する。
Pythonを用いたビジュアル作成の手順を詳細に説明します。
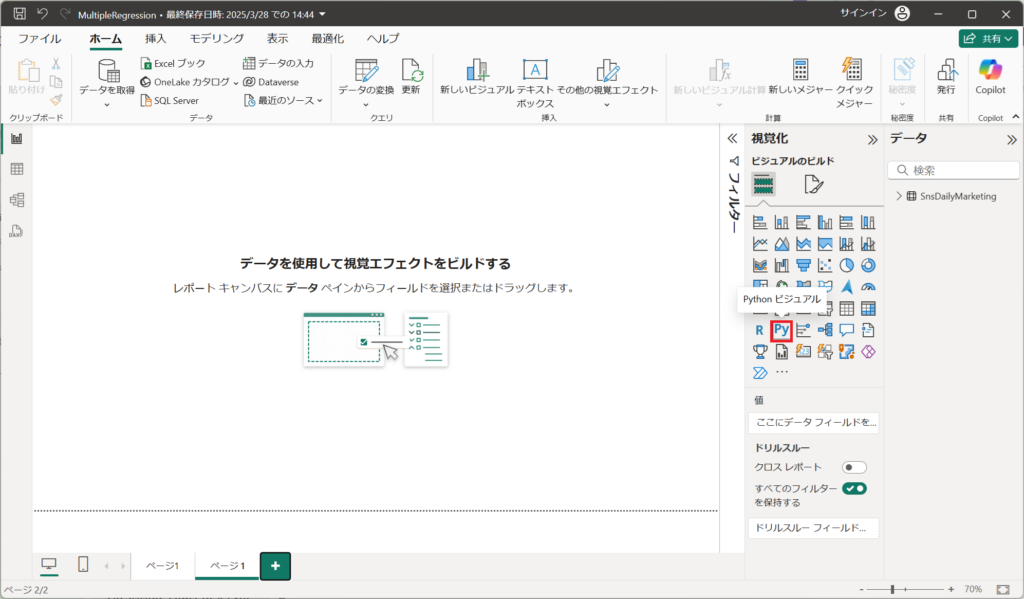
①.ビジュアルより「Python ビジュアル」を選択する。
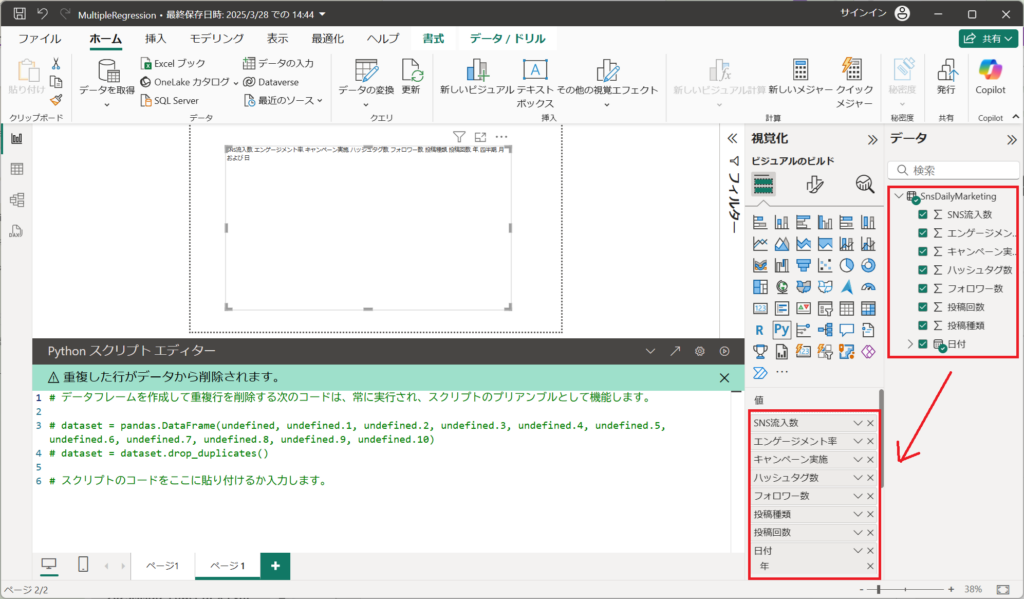
②.使用したいテーブルの列を設定する。
※今回はSnsDailyMarketingテーブルの列をすべて選択する。
③.Pythonコードを画面中央下のPythonスクリプト エディターへ入力する。
④.コードを入力する。
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from datetime import datetime
import matplotlib.dates as mdates
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score, mean_squared_error
import statsmodels.api as sm
# データ前処理
matplotlib.rcParams['font.family'] = 'Meiryo'
dataset = dataset.dropna()
dataset["日付"] = pd.to_datetime(dataset["日付"])
# 説明変数と目的変数
X = dataset[["投稿回数", "フォロワー数", "エンゲージメント率", "ハッシュタグ数", "投稿種類", "キャンペーン実施"]]
Y = dataset["SNS流入数"]
# 訓練データとテストデータに分割(80%:20%)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)
# データの標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 重回帰モデルの学習
model = LinearRegression()
model.fit(X_train, Y_train)
# statsmodels による P値の算出
X_train_sm = sm.add_constant(X_train)
ols_model = sm.OLS(Y_train, X_train_sm).fit()
# 回帰係数とP値を取得(小数点第3位まで)
coef_df = pd.DataFrame({
"変数": ["定数"] + X.columns.tolist(),
"回帰係数": [round(ols_model.params[0], 3)] + [round(v, 3) for v in ols_model.params[1:].tolist()],
"p値": [round(ols_model.pvalues[0], 3)] + [round(v, 3) for v in ols_model.pvalues[1:].tolist()]
})
# テストデータで予測
Y_pred = model.predict(X_test)
# モデルの評価
r2 = r2_score(Y_test, Y_pred)
rmse = np.sqrt(mean_squared_error(Y_test, Y_pred))
# 2025年のデータ取得
dataset_2025 = dataset[(dataset["日付"] >= "2025-01-01") & (dataset["日付"] <= "2025-12-31")].copy()
# 2026年用のデータ作成
dataset_2026 = dataset_2025.copy()
dataset_2026["日付"] = dataset_2026["日付"] + pd.DateOffset(years=1)
# 2026年の予測
dataset_2026_X = dataset_2025[["投稿回数", "フォロワー数", "エンゲージメント率", "ハッシュタグ数", "投稿種類", "キャンペーン実施"]]
dataset_2026_X = scaler.transform(dataset_2026_X) # 標準化適用
dataset_2026_Y = model.predict(dataset_2026_X)
# 予測結果をデータフレームにまとめる
forecast_df = dataset_2026[["日付"]].copy()
forecast_df["予測SNS流入数"] = dataset_2026_Y
# --- 可視化 ---
fig, ax = plt.subplots(figsize=(14, 6))
sns.lineplot(x=dataset["日付"], y=dataset["SNS流入数"], label="実測値", color="blue", ax=ax)
sns.lineplot(x=forecast_df["日付"], y=forecast_df["予測SNS流入数"], label="予測値", color="red", linestyle="dashed", ax=ax)
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=3))
plt.xticks(rotation=30)
ax.set_xlabel("日付")
ax.set_ylabel("SNS流入数")
ax.set_title("SNS流入数の予測")
ax.legend(loc="upper left")
ax.grid()
ax.set_ylim(0, 300)
# R²とRMSEをグラフの右下に追加
text_str = f"R²: {r2:.3f}\nRMSE: {rmse:.3f}"
ax.text(0.75, 0.1, text_str, transform=ax.transAxes, fontsize=12,
verticalalignment='bottom', bbox=dict(boxstyle='round', facecolor='white', alpha=0.5))
# --- テーブルを右側に表示 ---
table_data = coef_df.values.tolist()
table_data.insert(0, ["変数", "回帰係数", "p値"])
# テーブルの配置
table = plt.table(cellText=table_data, colLabels=None, loc="upper right", cellLoc="center", bbox=[0.65, 0.65, 0.35, 0.35])
# テーブルのフォントサイズと背景色を設定
table.auto_set_font_size(False)
table.set_fontsize(9)
for key, cell in table.get_celld().items():
cell.set_facecolor('white')
cell.set_edgecolor('black')
plt.show()
⑤コードを解説します。
1.ライブラリのインポート
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from datetime import datetime
import matplotlib.dates as mdates
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score, mean_squared_error
import statsmodels.api as sm・データ操作、可視化、機械学習モデルの構築・評価、統計解析に必要なライブラリをインポートしています。
・matplotlibとseabornを用いてグラフを描画。
・scikit-learnで重回帰分析を行い、評価指標(R²スコア、RMSE)を計算。
・statsmodelsで回帰係数とP値を計算します。
2.データ前処理
matplotlib.rcParams['font.family'] = 'Meiryo'
dataset = dataset.dropna()
dataset["日付"] = pd.to_datetime(dataset["日付"])・Meiryoフォントを使用して、日本語表示に対応。
・欠損値を削除し、日付列を日時形式に変換。
・分析対象がSNSデータであり、日付が含まれているため、時系列データとして扱います。
3.説明変数と目的変数の設定
X = dataset[["投稿回数", "フォロワー数", "エンゲージメント率", "ハッシュタグ数", "投稿種類", "キャンペーン実施"]]
Y = dataset["SNS流入数"]・説明変数(特徴量)はSNS投稿に関する指標を含み、目的変数は「SNS流入数」です。
・特徴量には投稿回数、フォロワー数、エンゲージメント率などを含めています。
4.データ分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)・データセットを訓練データとテストデータに8:2の割合で分割。
・random_state=42で乱数シードを固定し、再現性を確保。
5.データの標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)・重回帰分析ではスケールの違いがモデル性能に影響を与えるため、標準化(平均0, 分散1)を実施。
6.重回帰モデルの学習
model = LinearRegression()
model.fit(X_train, Y_train)・LinearRegressionクラスを使用してモデルを構築。
・訓練データに基づき、回帰係数を算出。
7.P値を求めるためのOLSモデル設定
X_train_sm = sm.add_constant(X_train)
ols_model = sm.OLS(Y_train, X_train_sm).fit()・statsmodelsでP値を求めるため、定数項を追加してOLSモデルを構築。
8.回帰係数とP値をデータフレームへ格納
coef_df = pd.DataFrame({
"変数": ["定数"] + X.columns.tolist(),
"回帰係数": [round(ols_model.params[0], 3)] + [round(v, 3) for v in ols_model.params[1:].tolist()],
"p値": [round(ols_model.pvalues[0], 3)] + [round(v, 3) for v in ols_model.pvalues[1:].tolist()]
})・回帰係数とP値をデータフレーム形式で表示し、見やすく整理。
9.モデル評価
Y_pred = model.predict(X_test)
r2 = r2_score(Y_test, Y_pred)
rmse = np.sqrt(mean_squared_error(Y_test, Y_pred))・モデルの予測精度をR²スコアとRMSEで評価。
10.2025年データの取得
dataset_2025 = dataset[(dataset["日付"] >= "2025-01-01") & (dataset["日付"] <= "2025-12-31")].copy()・datasetから2025年のデータのみを抽出し、新たなデータフレームとして格納しています。
・copy()を使うことで、元のデータを変更せず、独立したコピーを作成しています。
11.2026年データの作成
dataset_2026 = dataset_2025.copy()
dataset_2026["日付"] = dataset_2026["日付"] + pd.DateOffset(years=1)・2025年データをコピーしてdataset_2026を作成。
・日付を1年後にシフトさせて、2026年のデータとして扱う
・pd.DateOffset(years=1)を利用して、全ての日時を1年後に更新する
12.2026年の流入数予測
dataset_2026_X = dataset_2025[["投稿回数", "フォロワー数", "エンゲージメント率", "ハッシュタグ数", "投稿種類", "キャンペーン実施"]]
dataset_2026_X = scaler.transform(dataset_2026_X) # 標準化適用
dataset_2026_Y = model.predict(dataset_2026_X)・2025年データから、モデル学習に使用した説明変数(特徴量)を抽出。
・学習時と同じscalerオブジェクトを使用して、2026年のデータを標準化。
・学習済みモデルを用いて、2026年のSNS流入数を予測する。
13.予測結果をデータフレームにまとめる
forecast_df = dataset_2026[["日付"]].copy()
forecast_df["予測SNS流入数"] = dataset_2026_Y・2026年の日付を持つデータフレームに、予測結果(SNS流入数)を追加。これにより、日付と予測値がセットになったデータフレームを作成する。
14.予測結果の可視化
fig, ax = plt.subplots(figsize=(14, 6))
sns.lineplot(x=dataset["日付"], y=dataset["SNS流入数"], label="実測値", color="blue", ax=ax)
sns.lineplot(x=forecast_df["日付"], y=forecast_df["予測SNS流入数"], label="予測値", color="red", linestyle="dashed", ax=ax)・実測値(青)と予測値(赤点線)を重ねて表示。
15.軸やグラフの調整
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=3))
plt.xticks(rotation=30)
ax.set_xlabel("日付")
ax.set_ylabel("SNS流入数")
ax.set_title("SNS流入数の予測")
ax.legend(loc="upper left")
ax.grid()
ax.set_ylim(0, 300)・X軸のフォーマットは年月形式(%Y-%m)に整形し、3か月ごとの目盛りを表示。
・軸ラベル、グラフタイトル、凡例、グリッドを設定。
・Y軸の範囲を0~300に固定。
16.R²スコアとRMSEの表示
text_str = f"R²: {r2:.3f}\nRMSE: {rmse:.3f}"
ax.text(0.75, 0.1, text_str, transform=ax.transAxes, fontsize=12,
verticalalignment='bottom', bbox=dict(boxstyle='round', facecolor='white', alpha=0.5))・グラフ内の右下に、モデル評価指標(R²とRMSE)を表示。
・白背景で強調し、見やすくしています。
17.結果テーブルの表示
table_data = coef_df.values.tolist()
table_data.insert(0, ["変数", "回帰係数", "p値"])18.テーブルの可視化
table = plt.table(cellText=table_data, colLabels=None, loc="upper right", cellLoc="center", bbox=[0.65, 0.65, 0.35, 0.35])
table.auto_set_font_size(False)
table.set_fontsize(9)
for key, cell in table.get_celld().items():
cell.set_facecolor('white')
cell.set_edgecolor('black')・グラフの右上に表示し、フォントサイズやセルの背景色を調整。
・枠線を黒に統一し、視認性を確保。
19.グラフの表示
plt.show()・実測値と予測値が一目で比較でき、2026年の流入数予測結果を確認できる。
⑥.コード入力後、実行ボタンを押下する。
4.画面描写されたことを確認して、完了です。
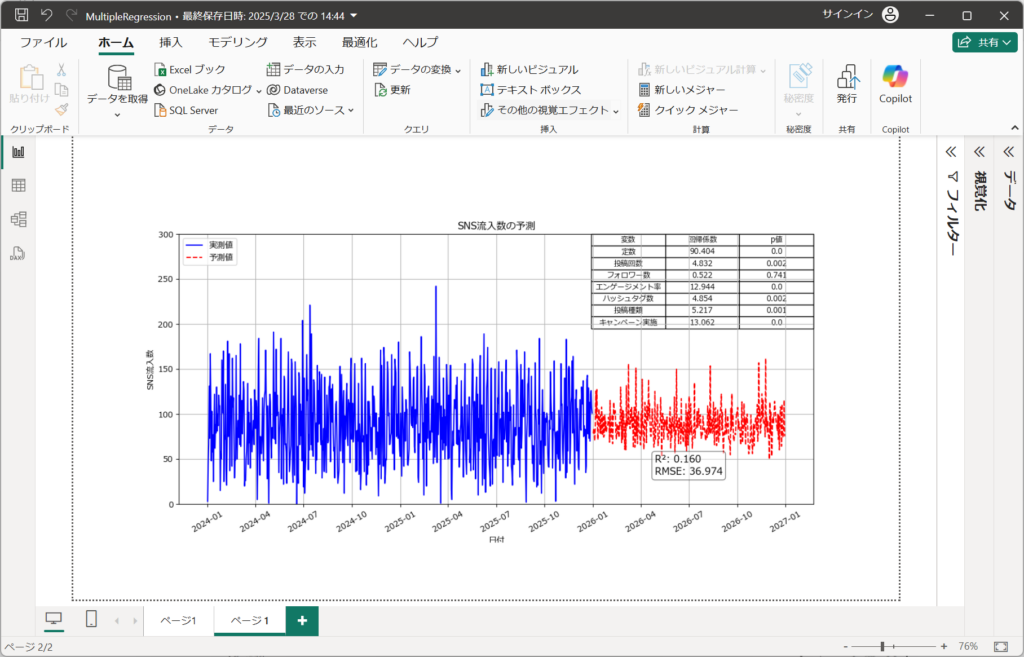
重回帰分析をビジュアルで表示しました。
引き続き、グラフの読み方を解説します。
まとめ(結論と今後の展望)
本記事では、Power BIとPythonを活用した重回帰分析について解説し、モデルの学習プロセスやそのメリット・デメリットについて触れた。重回帰分析を用いることで、複数の要因が目的変数にどのように影響を与えるのかを明確にし、より精度の高い予測が可能となる。実際に動かしてみて、Power BIとPythonの連携を活用し、より効果的なデータ活用を目指してみてください。

