目次
はじめに
「Power BI × Pythonで学ぶロジスティック回帰分析の実践」で作成したロジスティック回帰分析について解説します。ロジスティック回帰分析を実施したものの、結果の読み解き方がわからない方に向けて、詳しく説明します。
方法(アプローチ・使用技術)
前回のおさらい
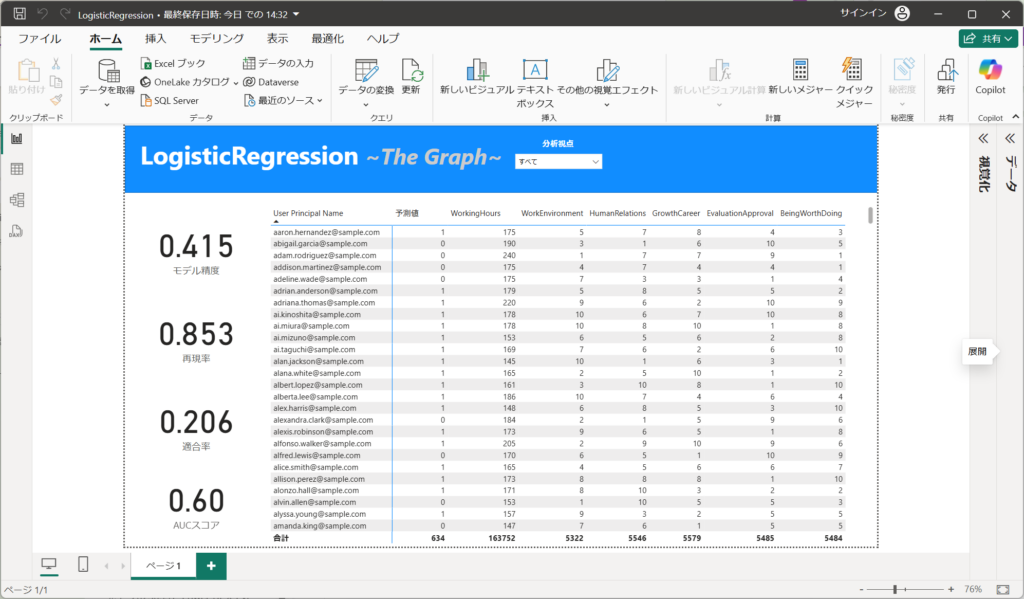
エンゲージメント調査データからロジスティック回帰分析で学習モデルの生成を行い、ビジュアルを作成しました。本記事はロジスティック回帰分析の読み解き方から始めます。
ロジスティック回帰分析の読み方
ロジスティック回帰(Logistic Regression)は、統計学および機械学習で広く用いられる分類アルゴリズムの一つです。特に、二値分類(二つのカテゴリにデータを分類する)に適しており、確率モデルとしても活用されます。線形回帰とは異なり、ロジスティック回帰ではシグモイド関数(sigmoid function)を使用して、出力を0から1の範囲に収めることで、確率的な解釈を可能にします。
精度を高めるためにすべきこと
ロジスティック回帰の精度を向上させるためには、以下のポイントに注意することが重要です。
- データの前処理
欠損値の補完や、カテゴリ変数の適切なエンコーディング(例:ワンホットエンコーディング)、標準化(正規化)を行うことで、モデルの学習をスムーズに進めることができます。※今回は標準化を組み込んでいます。 - 適切な閾値の設定
ロジスティック回帰では、確率が一定の閾値を超えた場合に「1」、そうでない場合に「0」と分類します。
モデルを使って確率を予測し、閾値を適用して予測結果を決定します。
予測値 > 閾値 ・・・1
予測値 ≦ 閾値 ・・・0
この閾値の調整により、モデルのパフォーマンスが決まります。 - 適切な特徴量の選択
特徴量の選択は、モデルの性能を大きく左右します。しかし、特徴量をはじめから決めることは非常に難しいです。変数の寄与度を見つつ、チューニングを施します。
1.データの前処理
データの標準化について
ロジスティック回帰を含む多くの機械学習アルゴリズムでは、データのスケールが異なると学習が不安定になることがあります。そのため、データの標準化を行うことが推奨されます。
標準化とは
標準化(Standardization)は、各特徴量の平均を0、標準偏差を1に調整する処理です。これにより、エンゲージメントスコア(1~10)や勤怠時間(NN hours)など、異なるスケールの特徴量を統一し、学習の安定性を向上させます。
標準化は以下の式で計算されます。
X' = (X - μ) / σ
ここで、
・X は元の特徴量の値
・μ は特徴量の平均
・σ は特徴量の標準偏差
・X' は標準化後の値
以下の設定にてスケール調整を行っています。
# 標準化(スケール調整)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)2.適切な閾値の設定
ロジスティック回帰のモデルを評価する際には、さまざまな指標が用いられます。それぞれの指標を理解し、適切に活用することが、モデルの最適化には不可欠です。
混合行列
指標の理解において混合行列をまずは解説します。混同行列とは、以下の点を表にしたものです。
・モデルの予測値が陽性か陰性か
・実際の値が陽性か陰性か
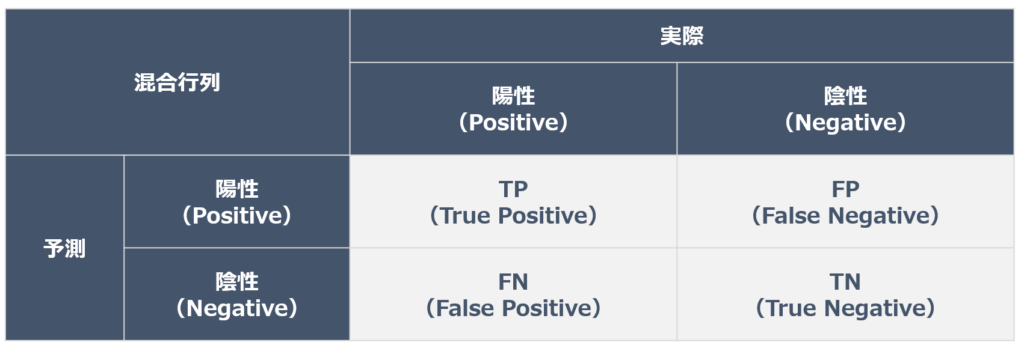
モデルが正しく予測したパターンは、先頭にT(True)がつきます。
TP(True Positive):モデルが陽性と予測し、実際も陽性だった
TN(Ture Negative):モデルが陰性と予測し、実際も陰性だった
モデルが間違って予測したパターンは、先頭にF(False)がつきます。
FP(False Positive):モデルが陽性と予測し、実際は陰性だった
FN(False Negative):モデルが陰性と予測し、実際は陽性だった
これらの理解のもと、モデルの指標を解説します。
Accuracy(正解率)とは
Accuracy(正解率※)は、モデルが正しく分類できたデータの割合を示す指標です。言い換えると、「全体の中で正しく予測できた割合」です。
以下の式で計算されます。
Accuracy = (TP + TN) / (TP + TN + FP + FN)
- TP(True Positive):正例を正しく予測した数
- TN(True Negative):負例を正しく予測した数
- FP(False Positive):負例を誤って正例と予測した数
- FN(False Negative):正例を誤って負例と予測した数
※今回のPower BI の列名は「モデル精度」と表現しています。
例えば、100件のメールのうち、実際に迷惑メールである50件をすべて正しく検出し、普通のメール50件のうち45件を正しく判断できた場合、Accuracyは(50+45)/100 = 0.95(95%)です。
見方を変えると、「迷惑メールが1%しかない場合」に99%のAccuracyでも意味がないことがあります。これは「ほとんど普通のメール」と予測しているだけだからです。Accuracyは分かりやすい指標ですが、クラスの不均衡(例:陽性ラベルが少ない場合)に弱いため、他の指標と組み合わせて評価することが重要です。
Precision(適合率)とは
Precision(適合率)は、モデルが「正例」と予測したデータのうち、実際に正例であった割合を示します。例えを使って言い換えると、「迷惑メールと予測した中で、本当に迷惑メールであった割合」です。
Precision = TP / (TP + FP)
例えば、100通のメールを迷惑メールと判断したうち、実際に80通が迷惑メールだったとします。Precisionは80/100 = 0.8(80%)です。誤って迷惑メールと判断するとPrecisionが低くなります。Precisionが高いと「迷惑メールと判断したらほぼ間違いない」と言えます。例えば、薬の副作用を検出するモデルでは、誤検出が少ない方が良いため、Precisionが重要な指標となります。
Recall(再現率)とは
Recall(再現率)は、実際に正例であるデータのうち、モデルが正例と予測できた割合を示します。言い換えると、「実際の迷惑メールの中で、どれだけ正しく見つけられたか」です。
Recall = TP / (TP + FN)
例えば、50通の迷惑メールがあり、そのうち40通を正しく迷惑メールと判断できた場合、Recallは40/50 = 0.8(80%)です。見逃しが多いとRecallが低くなります。Recallが高いと「見逃しが少ない」と言えます。特に、病気を検出するモデルでは、見逃すと命に関わるため、False Negative(見逃し)を最小限にしたいケースで重要です。
F1スコアとは
F1スコアは、PrecisionとRecallのバランスを考慮した指標であり、以下の式で計算されます。
F1 = 2 × (Precision × Recall) / (Precision + Recall)
例えば、Precisionが0.8でRecallが0.6の場合、F1スコアは2 * (0.8 * 0.6) / (0.8 + 0.6) = 0.69です。バランスが良いときにF1スコアが高くなります。F1スコアは、PrecisionとRecallのトレードオフを考慮しながら「全体のバランスを評価する」ため、クラスの不均衡がある場合にも有用な指標となります。
AUC(Area Under the Curve)スコアとは
AUCスコアは、ROC(Receiver Operating Characteristic)曲線の下の面積を示す指標です。ROC曲線は、True Positive Rate(TPR, Recall)とFalse Positive Rate(FPR)の関係を表したグラフであり、モデルの分類性能を包括的に評価できます。
AUCスコアは0〜1の範囲で示され、1に近いほど分類精度が高いことを意味します。
0.9~1.0: 非常によい(excellent)
0.8~0.9: よい(good)
0.7~0.8: まあまあ(fair)
0.6~0.7: よくない(poor)
0.5~0.6: 失敗(fail)
参考:[評価指標]AUC(Area Under the ROC Curve:ROC曲線の下の面積)とは?:AI・機械学習の用語辞典 - @IT
0.8以上のスコアを出すのは難しいと思いますので、まずは0.6~0.8を狙うのが良いかと思います。
AUCスコアは、クラスの不均衡がある場合でも適切に評価できるため、多くの分類問題で活用されます。
最適な閾値とは
ロジスティック回帰では、予測された確率値に基づき、一定の閾値(threshold)を超えた場合に「1」、それ以下の場合に「0」と分類します。一般的には0.5がデフォルトの閾値として用いられますが、実際にはPrecision、Recall、F1スコア、AUCなどを考慮しながら適切な閾値を選定することが重要です。そのため、閾値の最適化には、ROC曲線を活用しながら、業務要件に応じたバランスを取ることが求められます。
ソースコード内では、 ROC曲線から最適なしきい値を見つけるように組み込んでいます。
fpr, tpr, thresholds = roc_curve(y_test, y_prob)
optimal_idx = (tpr - fpr).argmax()
optimal_threshold = thresholds[optimal_idx]閾値は理論上、コード内で最適化されています。
ただし、出てきた数値をうのみにするのではなく、上記の基礎知識を押さえておき、各スコアを評価できるようになることが望ましいです。
3.適切な特徴量の選択
「Pythonスクリプトを実行する」のステップにて、「importance_df」を展開します。
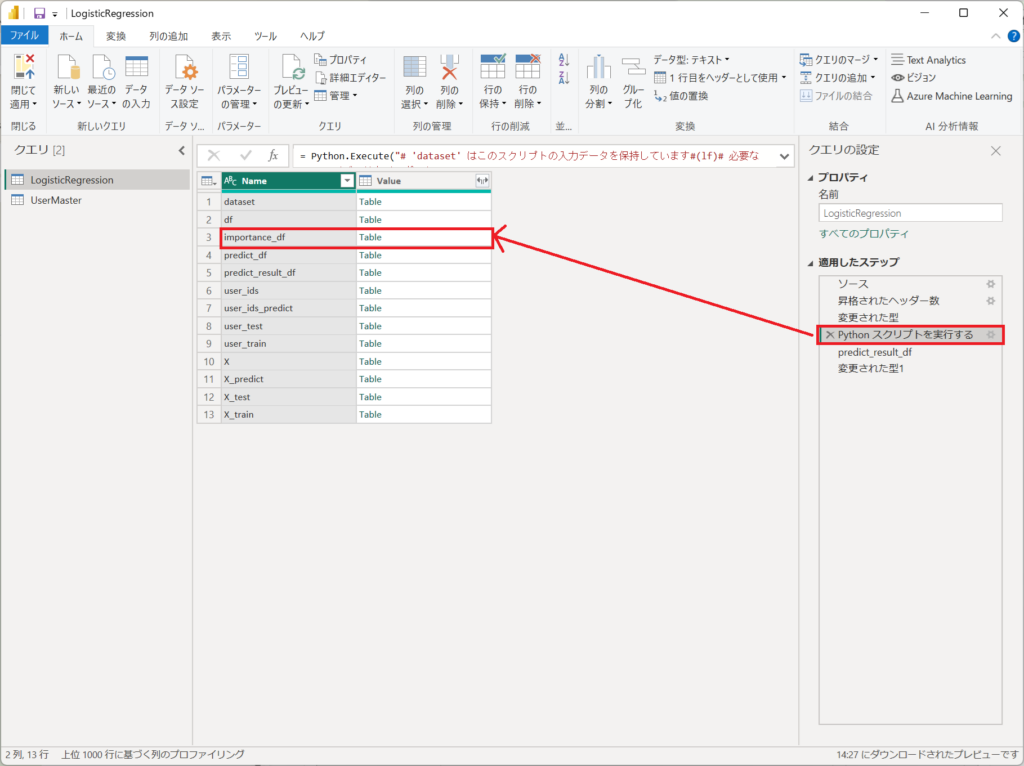
展開された結果から、ロジスティック回帰分析の線形変数が表示されます。
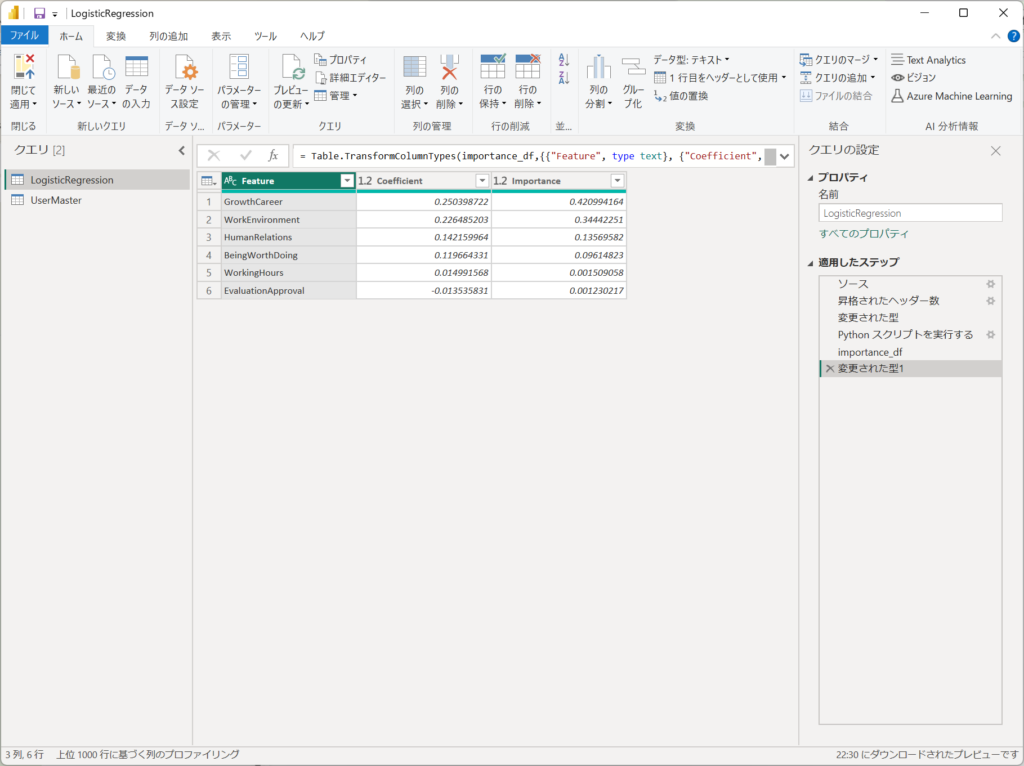
| Feature | Coefficient | Importance |
|---|---|---|
| GrowthCareer | 0.250398722 | 0.420994164 |
| WorkEnvironment | 0.226485203 | 0.34442251 |
| HumanRelations | 0.142159964 | 0.13569582 |
| BeingWorthDoing | 0.119664331 | 0.09614823 |
| WorkingHours | 0.014991568 | 0.001509058 |
| EvaluationApproval | -0.013535831 | 0.001230217 |
Coefficient(係数)
Coefficient は、ロジスティック回帰モデルで学習された各説明変数の重み(回帰係数)を示します。この値は 目的変数(JobRotationReserve)に対する各説明変数の影響の強さと方向 を表します。
- 正の値: 目的変数(JobRotationReserve = 1)になる確率を増加させる要因
- 負の値: 目的変数(JobRotationReserve = 1)になる確率を減少させる要因
Importance(寄与度)
Importance は、各説明変数がモデルの予測にどれだけ寄与しているかを示します。
具体的には、以下の式で計算しています。
Importance=(Coefficient×標準偏差)^2
- Importance が大きい変数 → 目的変数に対する影響が強い
- Importance が小さい変数 → 目的変数に対する影響が弱い
今回のケースでいうと、GrowthCareer と WorkEnvironment の2つの変数で全体の約76%の寄与度を持っている と読み取れます。つまり、この2つの変数が JobRotationReserve の予測において支配的な要因となっている と考えられます。
特に WorkingHours や EvaluationApproval の Importance が 1% 未満であることから、これらの変数は JobRotationReserve に対する寄与度がほぼ無視できるレベルである 可能性が高いです。
もし変数の削減を検討する場合、寄与度が極端に小さい変数を除外しても、モデルの予測精度に大きな影響を与えない可能性がある ため、次のステップとして特徴量選択を行うのも良いです。
グラフを読み解く
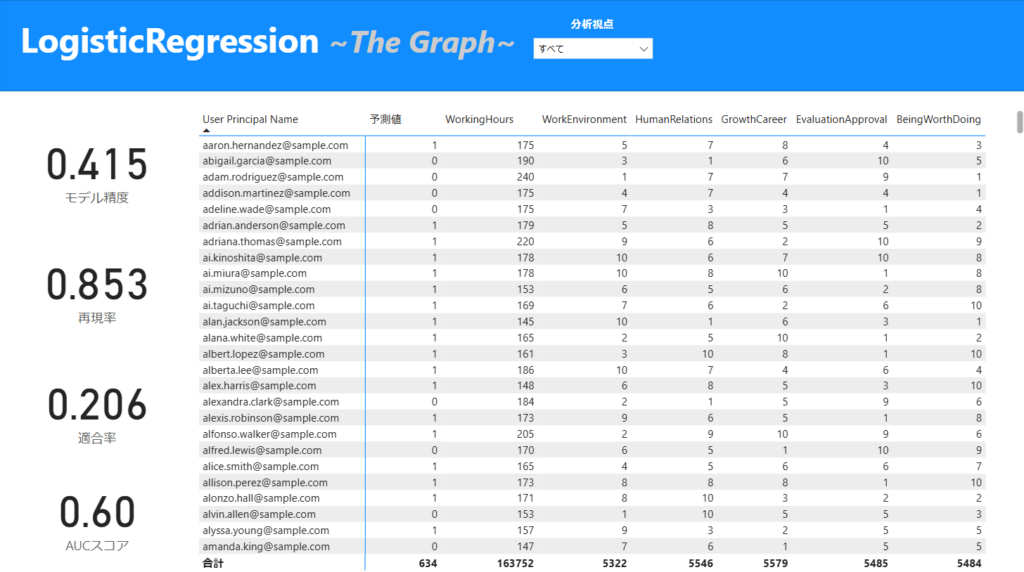
今回の予測モデルの評価をすると以下のようになります。
・Accuracy:0.415
全体の正解率が低く、モデルの全般的な予測性能は良くない可能性がある。
・Recall:0.853
再現率が高いため、実際に「陽性(1)」であるデータを多く正しく識別できている。
これはPrecisionが低いことからも多く陽性を判別しているため、数値が高めに出ている。
・Precision:0.206
適合率が低いため、陽性と予測したものの中に誤りが多い。
・AUCスコア:0.6
ROC曲線の下の面積(AUC)が0.6と低めであり、分類能力はあまり高くない。
あまりモデルとしては、高い精度を持っていません。画面中央の予測結果からも"予測値"に「1」が多く、予測精度に見直しが必要であることがわかります。不要な特徴量の削減や、不要なレコード(行)の見直しなど、モデルの精度向上が必要です。
まとめ(結論と今後の展望)
本記事では、Power BIとPythonを用いたロジスティック回帰を解説しました。ロジスティック回帰は、二値分類において強力な手法であり、適切な特徴量選択、データ前処理、正則化、閾値設定、および評価指標の活用がモデルの精度向上に不可欠です。Accuracy、Precision、Recall、F1スコア、AUCスコアなどの指標を理解し、最適な閾値を選定することで、実践的なモデルの構築に生かしていただけますと幸いです。
